
La paradoja de cumpleaños, también conocida como el problema del cumpleaños, es un hallazgo matemático que plantea la probabilidad de que dos personas en un grupo compartan la misma fecha de cumpleaños. Aunque pueda parecer sorprendente, la probabilidad de que esto suceda en un grupo de solo 23 individuos es del 50%. Es importante decir que en sentido estricto no se trata de una paradoja, ya que no es una contradicción lógica sino una verdad matemática que contradice la intuición que dicta el sentido común.
Para conocer más sobre el cálculo de esta probabilidad, desde Portal Universidad se pusieron en contacto con Alejandro Quintero, doctor en Matemáticas y docente de la Universidad Nacional de Mar del Plata.
En primer lugar, Quintero explicó por qué no se trata de una paradoja y dijo: “una paradoja es un razonamiento lógico que es correcto pero que cuando se lleva a la práctica no ocurre. El ejemplo más común es la famosa fábula de la tortuga y la liebre. Esta paradoja, que viene de la época de Zenón, plantea que la liebre está tan segura de que va a ganar que le deja una hora de ventaja a la tortuga. La tortuga recorre una cierta distancia en esa hora y la liebre sale, pero cuando la liebre llega al lugar donde se encontraba la tortuga cuando inició su carrera, la tortuga ya ha recorrido otro trecho, y así sucesivamente, por lo cual no debería alcanzarla nunca. Ese pensamiento donde la liebre nunca alcanza a la tortuga no se condice con la realidad: en la práctica la liebre si ganaría. Lo del cumpleaños no es una paradoja porque la probabilidad es un número que representa qué chances hay de que ocurra algo y puede ser que ocurra o no. No hay ninguna contradicción en ese razonamiento que se hace”.
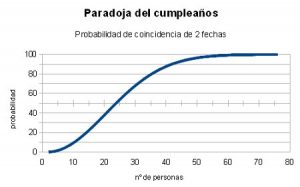
Foto: En un grupo de 23 personas, la probabilidad de que dos de ellas cumplan años el mismo día es del 50%.
En cuanto al cálculo concreto que se debe hacer para conocer esta probabilidad, Quintero dijo: “Generalmente para calcular la probabilidad lo que se hace es un estudio para ver cuántos casos son favorables sobre cuántos casos hay en total. En este caso lo que se hace es pensar al revés el problema: se calcula cuál es la probabilidad de que no cumplan el mismo día y con esa información se obtiene la probabilidad de que si cumplan el mismo día, porque la suma de esas probabilidad tiene que dar uno. La probabilidad en matemática va entre 0 y 1, por ejemplo si uno tira una moneda, la probabilidad de que salga cara será del 50% y de que salga cruz también, si sumamos ambas probabilidades tenemos el 100%. En este caso lo que se hace es tomar a una persona cualquiera y sabemos que su cumpleaños puede tener lugar en uno de 365 días. Si quiero saber la probabilidad de que la segunda no cumpla el mismo día, me quedan 364 días, si agarro una tercera persona 363 días y así sucesivamente. De este modo uno puede seguir analizando, dependiendo de la cantidad de gente que haya en el lugar”.
“Para el caso de dos personas, habría que calcular 365 x 364 y dividirlo por el resultado de 365 x 365. Este cálculo nos da que existe un 99,72% de que esas personas no cumplan años el mismo día, es decir un 0,28% de probabilidades de que sí lo hagan . Si multiplicamos 365 x 364 x 363 y proseguimos nos vamos a encontrar con que un momento la probabilidad comienza a ser muy alta. Si lo hacemos con 23 personas llegamos a este resultado donde ya es del 50%. A medida que aumenta el tamaño del grupo, la probabilidad aumenta exponencialmente, lo que nos lleva a reflexionar sobre la aleatoriedad y las probabilidades en nuestro mundo cotidiano”, explicó.
Este problema matemático puede parecer trivial, pero tiene aplicaciones prácticas en diversos campos. Sobre este aspecto, Quintero dijo: “Esto es una curiosidad matemática porque atenta contra la intuición. La probabilidad es una herramienta muy utilizada y no sólo en campos de análisis complejos sino también en cuestiones muy cotidianas como por ejemplo en los juegos de azar. En los casinos se usa la probabilidad para que los juegos siempre den ventaja a la banca por sobre el jugador. Un ejemplo de esto es el cero en la ruleta: es una casilla que no corresponde a ningún número ni color y se encuentra en una posición especial en el tablero”.

Foto: La probabilidad es una herramienta muy utilizada y no sólo en campos de análisis complejos sino también en cuestiones muy cotidianas como por ejemplo en los juegos de azar. Fuente: Télam.
“Si un jugador apuesta por un número específico y acierta, su ganancia sería de 35 veces la apuesta, ya que se paga 35 a 1. Sin embargo, las probabilidades reales de acertar un número específico son de 37 a 1, lo que significa que la probabilidad de perder es del 97,3%. En otras palabras, la presencia del 0 significa que siempre hay una probabilidad adicional de perder. Ahí es donde las empresas de juegos de azar usan la matemática para ver qué tipo de juego les conviene usar”, concluyó.
Fuente: Portal Universidad
Foto ilustrativa: Devin Young





